




 icons explained
icons explained[ periodic orbit theory | transitions to chaos | chaos books | quantum field theory | field theory book | group theory | in progress | miscelania ]
  |
My research, in plain words |
    icons explained
icons explained |
arXiv - Google Scholar - INSPIRE citations |
[ chaotic field theory | spatiotemporal theory | turbulence | symmetries of dynamics | Kuramoto-Sivashinsky | periodic orbits extraction | noise | wave chaos | modulated amplitude waves | periodic orbits from data | kill periodic orbits | nonhyperbolic dynamics | phase transitions | deterministic diffusion | cycle expansions | quantum determinants | geometry of chaos ]
 
| Periodic orbit research overview |

| Abstract of a general colloquium on the periodic orbit theory |
| Chaotic field theory |
Program whose goal is a theory of turbulent dynamics of classical, stochastic and quantum fields. Chaotic field theory is developed in two directions: 1) explorations of the feasibility of describing weak turbulence in terms of spatiotemporally recurrent patterns, and 2) new perturbation theory methods for computing corrections about nontrivial saddles of path integrals.
Read the sketch paper first, perhaps click through the trace formulas seminar next.
  
|
Predrag Cvitanović
Chaotic Field Theory: a sketch, Physica A 288 , 61 (2000) [ arXiv:nlin.CD/0001034 | DOI | NSF review panel critique ] |
| Spatiotemporal theory of turbulence |
We have been doing it all wrong. Junk your forward-in time integrators: a deterministic, from the equations up, no statistical assumptions theory of turbulence requires a spatiotemporal formulation.

| A deep dive into turbulence in spacetime: seminars, papers and notes |  |
H. Liang and P Cvitanović
A chaotic lattice field theory in one dimension J. Phys. A 55, 304002 (2022) [ arXiv:2201.11325 | DOI ] |
Our spacetime discretized model field theory, modern formulation. |  |
B Gutkin, P Cvitanović, R Jafari, A K Saremi and L Han
Linear encoding of the spatiotemporal cat map Nonlinearity 34, 2800--2836 (2021) [ arXiv:1912.02940 | DOI ] |
Our spacetime discretized model field theory, pre-1969 Soviet style approach. |
|
State space geometry of moderate |
Getting hang of turbulence for plumbers: pipes and planes. Program manifesto, gentle multimedia introduction, a few talks.
Planes and pipes: technical papers
 
|
N. Burak Budanur, Kimberly Y. Short,
Mohammad Farazmand, Ashley P. Willis
and
Predrag Cvitanović
Relative periodic orbits form the backbone of turbulent pipe flow [ arXiv:1705.03720 ] |
 
|
Ashley P. Willis,
Kimberly Y. Short,
and
Predrag Cvitanović
Symmetry reduction in high dimensions, illustrated in a turbulent pipe Phys. Rev. E 93, 022204 (2016) [ arXiv:1504.05825 ] |
 
|
Ashley P. Willis,
Predrag Cvitanović
and Marc Avila
Revealing the state space of turbulent pipe flow by symmetry reduction J. Fluid Mech. 721, 514-540 (2013) [ arXiv:1203.3701 ] |
   
|
John F. Gibson,
Jonathan Halcrow
and
Predrag Cvitanović
Visualizing the geometry of state space in plane Couette flow J. Fluid Mech. 611, 107 (2008) [ arXiv:0705.3957 ] |
 
|
John F. Gibson,
Jonathan Halcrow,and
Predrag Cvitanović
Equilibrium and traveling-wave solutions of plane Couette flow J. Fluid Mech. 638, 243 (2009) [ arXiv:0808.3375 ] |

|
Jonathan Halcrow,
John F. Gibson,
Predrag Cvitanović
and
Divakar Viswanath
Heteroclinic connections in plane Couette flow J. Fluid Mech. 621, 365 (2009) [ arXiv:0808.1865 ] |

|
Divakar Viswanath
and
Predrag Cvitanović
Stable manifolds and the transition to turbulence in pipe flow J. Fluid Mech. 627, 215 (2009) [ arXiv:0801.1918 ] |
| State space geometry of Kuramoto-Sivashinsky flow |
Explorations of weak turbulence described in terms of spatiotemporally recurrent patterns.
  
|
Xiong Ding, H. Chaté, Predrag Cvitanović, Evangelos Siminos, and K. A. Takeuchi
Estimating dimension of inertial manifold from unstable periodic orbits Phys. Rev. Lett. 117, 024101 (2017) [ arXiv:1604.01859 | DOI ] |
|
 
|
Predrag Cvitanović, Ruslan L. Davidchack and Evangelos Siminos
On state space geometry of the Kuramoto-Sivashinsky flow in a periodic domain SIAM J. Appl. Dyn. Syst. 9, 1 (2010) [ arXiv:0709.2944 ] |

|
Yueheng Lan and Predrag Cvitanović
Unstable recurrent patterns in Kuramoto-Sivashinsky dynamics Phys. Rev. E 78, 026208 (2008) [ arXiv:0804.2474 ] |
  
|
Predrag Cvitanović, Freddy Christiansen and Vahtang Putkaradze
Hopf's last hope: spatiotemporal chaos in terms of unstable recurrent patterns Nonlinearity 10, 50 (1997) [ arXiv:chao-dyn/9606016 | NSF critique ] |


|
Predrag Cvitanović and Y. Lan
Turbulence and what to do about it (Bristol, Gottingen 2004 - PDF overheads) |


|
Predrag Cvitanović
Spatiotemporal chaos in terms of unstable recurrent patterns (overheads + , seminar abstract) |

|
Related links: Vachtang Putkaradze
PhD thesis
The initial attempt: Vachtang's term paper 
|
Why ``Hopf's last hope'' in the title?
|
| Symmetries of dynamical systems |
How to quotient a symmetry of an equvariant dynamical system, rewrite the dynamics in the reduced, invariant coordinates.
This was meant to be a brief explanatory section in the ChaosBook.org chapter on trace formulas for systems with a continuous symmetry. Instead, I have gone the way of Marsdenites and am writing one paper after the other, each one looking very much like the preceeding one to a vulgar eye. Hopefully this all will eventually get digested into a single chapter of ChaosBook.org, and be done with.

|
N. Burak Budanur and Predrag Cvitanović
Unstable manifolds of relative periodic orbits in the symmetry-reduced state space of the Kuramoto-Sivashinsky system J. Stat. Phys. , (2016) [ arXiv:1509.08133 | ReadCube | DOI ] |

|
N. Burak Budanur, D. Borrero-Echeverry and Predrag Cvitanović
Periodic orbit analysis of a system with continuous symmetry - A tutorial Chaos 25, 073112 (2015) [ arXiv:1411.3303 | DOI ] |

|
N. Burak Budanur, Predrag Cvitanović,
Ruslan L. Davidchack and Evangelos Siminos
Reduction of the SO(2) symmetry for spatially extended dynamical systems [ arXiv:1405.1096 ] |

|
Predrag Cvitanović, Daniel Borrero-Echeverry, Keith Carroll,
Bryce Robbins and Evangelos Siminos
Cartography of high-dimensional flows: A visual guide to sections and slices Chaos 22, 047506 (2012) [ arXiv:1209.4915 ] |

|
Predrag Cvitanović
Got symmetry? here is how you slice it Classics Illustrated version of the above paper. |

|
Stefan Froehlich and Predrag Cvitanović
Reduction of continuous symmetries of chaotic flows by the method of slices Comm. Nonlinear Sci. and Numer. Simul. 17, 2074–2084 (2012) [ DOI | arXiv:1101.3037 ] |

|
Predrag Cvitanović, Ashley P. Willis and Marc Avila
Revealing the geometry of turbulent pipe flow attractor by symmetry reduction in Jianxiang Wang, ed., Proceed. ICTAM 2012 Intern. Congr. Theor. and Appl. Mech. (2012) [ the long paper is here ] |

|
Evangelos Siminos and Predrag Cvitanović
Continuous symmetry reduction and return maps for high-dimensional flows Physica D 240, 187-198 (2011) [ arXiv:1006.2362 ] |

|
Predrag Cvitanović
Relativity for cyclists ChaosBook.org A (hopefully) pedagogical overview of the symmetry reduction methods. |

|
Predrag Cvitanović
Continuous symmetry reduction for high-dimensional flows Attempt to motivate the need for symmetry reduction, and the available methods in a few slides. |



|
Predrag Cvitanović
Continuous symmetry reduced trace formulas (in preparation, July 2006) Why is this paper not published yet? I would like at least one person out there in the universe to understand it before submitting it. Seems to be a high treshold. |


|
Predrag Cvitanović and Bruno Eckhardt
Symmetry decomposition of chaotic dynamics Nonlinearity 6, 277 (1993) [ arXiv:chao-dyn/9303016 ] in part superceeded by ChaosBook.org: World in a mirror |
| Modulated amplitude waves |
Getting hang of spatiotemporal dynamics in nearly integrable regimes, as a warmup to turbulent dynamics...

|
Mason A. Porter
and
Predrag Cvitanović
A perturbative analysis of Modulated Amplitude Waves in Bose-Einstein Condensates CHAOS 14, 739 (2004) [ arXiv:nlin.CD/0308024 ] |

|
Mason A. Porter
and
Predrag Cvitanović
Modulated Amplitude Waves in Bose-Einstein Condensates Phys. Rev. E 69, 047201 (2004) [ arXiv:nlin.CD/0307032 ] |

|
Yueheng Lan,
Nicola Garnier and
Predrag Cvitanović
Modulated solutions of the complex Ginzburg-Landau equation Physica D 188 193, (2004) [ arXiv:nlin.ps/0208001 ] |
| Noise is your friend |
The noise that physical systems are affected by limits the resolution that can be attained in partitioning their state space. We determine the `finest attainable' partition and replace the Fokker-Planck evolution is by a finite matrix.
 |
Jeffrey M. Heninger, Domenico Lippolis and Predrag Cvitanović
Perturbation theory for the Fokker-Planck operator in chaos Comm. Nonlinear Sci. and Numer. Simul. 55, 16-28 (2017) [ DOI | arXiv:1507.00462 ] |
 |
Jeffrey M. Heninger, Domenico Lippolis and Predrag Cvitanović
Neighborhoods of periodic orbits and the stationary distribution of a stochastic chaotic systems Phys. Rev. E. 92 062922, (2015) [ arXiv:1507.00462 ] |

|
Predrag Cvitanović and
Domenico Lippolis
Knowing when to stop: How noise frees us from determinism in M. Robnik and V.G. Romanovski, eds., Let's Face Chaos through Nonlinear Dynamics, pp. 82--126 (Am. Inst. of Phys., Melville, New York, 2012) [ arXiv:1206.5506 ] |
|
Predrag Cvitanović
Physicist's life is intractable Intractability workshop: "Counting, Inference, and Optimization on Graphs", 2 nov 2011 (talk aimed at computer scientists) |
  | video of the intractable lecture (pretty clear on the interplay of noise and determinism - recommended) |

|
Domenico Lippolis and Predrag Cvitanović
How well can one resolve the state space of a chaotic flow? Phys. Rev. Lett. 104, 014101 (2010) [ arXiv:0902.4269 ] |

|
Predrag Cvitanović and Domenico Lippolis
How well can one resolve the state space of a chaotic flow? SIAM Snowbird Dynamical Systems 2011 talk. |
A triptych of technical papers whose goal is to develop improved methods of computing higher order corrections to nontrivial saddles of path integrals:

|
Predrag Cvitanović,
Carl P. Dettmann, Ronnie Mainieri and Gábor Vattay
Trace formulas for stochastic evolution operators: Weak noise perturbation theory J. Stat. Phys. 93, 981 (1998) [ chao-dyn/9807034 ] |

|
Predrag Cvitanović,
Carl P. Dettmann, Ronnie Mainieri and Gábor Vattay
Trace formulas for stochastic evolution operators: Smooth conjugation method Nonlinearity 12, 939 (1999) [ ps.gz published version , ps.gz , chao-dyn/9811003 ] |

|
Predrag Cvitanović,
Carl P. Dettmann, G. Palla, Niels Søndergaard and Gábor Vattay
Spectrum of stochastic evolution operators: Local matrix representation approach Phys. Rev. E 60, 3936 (1999) [ ps.gz , chao-dyn/9904027 ] |

|
Predrag Cvitanović
Trace formulas for stochastic evolution operators 
(seminar abstract, 1999). |

|
Predrag Cvitanović
Noisy Chaos a talk at Hans C. Fogedby 60 symposium. |
| Wave chaos in elastodynamics |
A step toward generalizing Gutzwiller semiclassical theory to wave chaos in elastodynamical systems (professionals do not allow us to call this "acoustics")

|
Predrag Cvitanović, Niels Søndergaard and Andreas Wirzba
Wave Chaos in Elastodynamic Cavity Scattering Europhysics Letters 72, 534 (2005) Brief history: submitted to Phys Rev Letters Aug 28 2001; revised version submitted May 18 2004; referee offended by the "In elastodynamics, period two implies chaos" title - rejected; submitted to Europhysics Letters, May 2005, revised version with more resonances included Sep 23 2005, accepted Sep 26 2005. [ arXiv:nlin/0108053 ] |
|
| Periodic orbit extraction |
How to compute Floquet exponents that differ by 1000's of orders of magnitude (a step toward determining physical dimension of inertial manifolds):

|
Xiong Ding
and
Predrag Cvitanović
Periodic eigendecomposition and its application in Kuramoto-Sivashinsky system [ arXiv:1406.4885 ] |
A variational principle for robust periodic orbit and invariant tori searches:

|
Yueheng Lan,
Cristel Chandre,
and
Predrag Cvitanović
Variational method for locating invariant tori Phys. Rev. E 74, 046206 (2006) [ arXiv:nlin.CD/0508026 ] |
 
|
Predrag Cvitanović
and
Yueheng Lan
Turbulent fields and their recurrences in N. Antoniou, ed., Proceed. of 10. Intern. Workshop on Multiparticle Production: Correlations and Fluctuations in QCD (World Scientific, Singapore 2003); [ arXiv:nlin.CD/0308006 ] |

|
Yueheng Lan
and
Predrag Cvitanović
Variational method for finding periodic orbits in a general flow Phys. Rev. E 69, 016217 (2004) [ arXiv:nlin.CD/0308008 | ps.gz ] |
| Periodic orbit extraction from data |
An early proposal on how to fish for periodic orbits by looking for near recurrences:

|
D. Auerbach, Predrag Cvitanović,
Jean-Pierre Eckmann, Gemunu Gunaratne and Itamar Procaccia
Exploring chaotic motion through periodic orbits Phys. Rev. Lett. 58, 2387-2389 (1987) |
An attempt to demonstrate existence of unstable periodic orbits and chaos in a slices of rat brains, very noisy neurophysiology experimental data
| Kill periodic orbit theory: |
Two papers demonstrating that periodic orbits must satisfy infinitely many sum rules

|
Predrag Cvitanović, Kim Hansen, Juri Rolf and Gabor Vattay
Beyond periodic orbit theory Nonlinearity 11, 1209 (1998) [ ps.gz ] |

|
Sune F. Nielsen, Per Dahlqvist and Predrag Cvitanović
Periodic orbit sum rules for billiards: Accelerating cycle expansions J. Phys. A 32, 6757 (1999) [ ps.gz , chao-dyn/9901001 , working notes ] |
| Nonhyperbolic dynamics |
Non-hyperbolicity, intermittency, power-law correlations: convergence of cycle expansions, analyticity of dynamical zeta functions, approach to the border of order by renormalization methods.

|
Roberto Artuso, Predrag Cvitanović and Gregor Tanner
Cycle expansions for intermittent maps Proc. Theo. Phys. Supp. 150, 1 (2003) [ nlin.CD/0305008 ] [most of this paper is incorporated in ChaosBook.org] |

|
Carl P. Dettmann and Predrag Cvitanović
Cycle expansions for intermittent diffusion Phys. Rev. E 56, 6687 (1997) |
   |
Roberto Artuso, Erik Aurell and Predrag Cvitanović
Recycling of strange sets: II. applications Nonlinearity 3, 361 (1990) |
| Deterministic diffusion |
Periodic orbit theory of deterministic diffusion

 |
Predrag Cvitanović, Jean-Pierre Eckmann and Pierre Gaspard
Transport properties of the Lorentz gas in terms of periodic orbits Chaos, Solitons and Fractals 6, 113 (1995) - (61 kB) [ ps.gz ] |

|
Predrag Cvitanović, Pierre Gaspard and Thomas Schreiber
Investigation of the Lorentz Gas in terms of periodic orbits CHAOS 2, 85 (1992) |
Periodic orbit theory of diffusion extended to power spectra, with Pikovsky and Feigenbaum. Both Mitchell's draft and Arkady's draft have interesting material not in the published, abreviated version:

|
Predrag Cvitanović
and
Arkady S. Pikovsky
Cycle expansion for power spectrum Proc. SPIE - Int. Soc. Opt. Eng. (USA) 2038, 290 (1997) |
| Cycle expansions |
How to implement the periodic orbit theory as a computational method

|
Predrag Cvitanović
Trace formulas in classical dynamical systems in I.V. Lerner, J.P. Keating, D.E. Khmelnitskii, eds., Supersymmetry and Trace Formulae: Chaos and Disorder, (Plenum, New York 1998) |

|
Gábor Simon,
Predrag Cvitanović,
Mogens T. Levinsen, I. Csabai and Á. Horváth
Periodic orbit theory applied to a chaotically oscillating gas bubble in water Nonlinearity 15, 25 (2002) |
Predrag Cvitanović,
Gábor Vattay
and
Andreas Wirzba
Quantum fluids and classical determinants in H. Friedrich and B. Gerhardt., eds., Classical, Semiclassical and Quantum Dynamics in Atoms - in Memory of Dieter Wintgen, Lecture Notes in Physics 485 (Springer, New York 1997) [ ps.gz , chao-dyn/9608012 ] |
 
|
Predrag Cvitanović Dynamical averaging in terms of periodic orbits Physica D 83, 109 (1995) [most of this paper is incorporated in ChaosBook.org] |
Neal J. Balmforth,
Predrag Cvitanović,
Glenn R. Ierley, Edward A. Spiegel and Gabor Vattay
|

|
Freddy Christiansen
and
Predrag Cvitanović
Periodic orbit quantization of the anisotropic Kepler problem CHAOS 2, 61 (1992) |

| Periodic orbit theory in classical and quantum mechanics, CHAOS 2, 1 (1992) |
| Kvantekaos, KVANT 5, 1 (1994) [e-print not available] |
| Kvantes Lykkelige Dag (with Kenneth Krabat), Naturligvis 20 (1991) [e-print not available] |


|
Predrag Cvitanović and Bruno Eckhardt
Periodic orbit expansions for classical smooth flows J. Phys A 24, L237 (1991) [ preprint ] |

|
Freddy Christiansen, Predrag Cvitanović and Hans Henrik Rugh
The spectrum of the period-doubling operator in terms of cycles J. Phys A 23, L713 (1990) |


|
Predrag Cvitanović and Bruno Eckhardt
Periodic orbit quantization of chaotic systems Phys. Rev. Lett. 63, 823 (1989) |
The two in-depth papers on cycle expansions combine Artuso and Aurell PhD theses with several years of my own work - mostly incorporated into ChaosBook.org since. Nobody reads the second paper, which is a pity - there is some good stuff there.
  
|
Roberto Artuso, Erik Aurell and Predrag Cvitanović
Recycling of strange sets: I. cycle expansions Nonlinearity 3, 325 (1990) |
The first paper on cycle expansions:



|
Predrag Cvitanović
Invariant measurement of strange sets in terms of cycles Phys. Rev. Lett. 61, 2729 (1988) |
| Quantum determinants |
For nice hyperbolic systems Fredhollm determinats are entire, but the Gutzwiller-Voros zeta functions have poles. In 1992 we conjectured a "quantum Fredholm determinant" and showed that it has a larger radius of analiticity than the Gutzwiller-Voros zeta function. Extension of the evolution from phase space to phase space together with the tangent space enables us to construct a multiplicative "quasiclassical evolution operator" and the associated (entire) "quasiclassical zeta function". Unfortunatelly this zeta function has extraneous "classical" eigenvalues, and is not useful in practice. Restriciting its function space to purely quantum spectrum remains an open problem.

|
Predrag Cvitanović,
Gábor Vattay
and
Andreas Wirzba
Quantum fluids and classical determinants in H. Friedrich and B. Gerhardt., eds., Classical, Semiclassical and Quantum Dynamics in Atoms - in Memory of Dieter Wintgen, Lecture Notes in Physics 485 (Springer, New York 1997) [ ps.gz , chao-dyn/9608012 ] |

|
Predrag Cvitanović,
Bruno Eckhardt,
Per E. Rosenqvist, Gunnar Russberg and P. Scherer
Pinball scattering in G. Casati and B. Chirikov, eds., Quantum Chaos, (Cambridge University Press, Cambridge 1994) [ ps.gz - sorry, no figures ] |

|
Predrag Cvitanović
and Gábor Vattay
Entire Fredholm determinants for evaluation of semi-classical and thermodynamical spectra Phys. Rev. Lett. 71, 4138 (1993) [ arXiv:chao-dyn/9307012 ] |

|
Predrag Cvitanović, Per E. Rosenqvist, Gábor Vattay, and Hans H. Rugh
A Fredholm determinant for semi-classical quantization CHAOS 3, 619 (1993) [ ps | arXiv:chao-dyn/9307014 ] |

|
Predrag Cvitanović
and
Per E. Rosenqvist
A new determinant for quantum chaos in G.F. Dell'Antonio, S. Fantoni and V.R. Manfredi, eds., From Classical to Quantum Chaos, Soc. Italiana di Fisica Conf. Proceed. 41, pp. 57-64 (Ed. Compositori, Bologna 1993) |
| Geometry of chaos |
How to partition the phase space of a chaotic dynamical system

|
Mason A. Porter
and
Predrag Cvitanović
Ground Control to Niels Bohr: Exploring Outer Space with Atomic Physics Notices Am. Math. Soc. 52, 1020 (2005) [ physics/0505085 , pdf ] Featured in: Science News |
 
|
Predrag Cvitanović
Periodic orbits as the skeleton of classical and quantum chaos Physica D 51 138 (1991) [most of this paper is incorporated in ChaosBook.org] |
  
|
Predrag Cvitanović, Gemunu H. Gunaratne and Itamar Procaccia
Topological and metric properties of Hénon-type attractors Phys. Rev. A 38, 1503 (1988) [the non-Procaccian, non-gibberish part of this paper is incorporated in ChaosBook.org] |

|
Predrag Cvitanović
and
Kai T. Hansen
Bifurcation structures in maps of Hénon type Nonlinearity 11, 1233 (1998) [the best exposition of physicist's pruning front theory is possibly still Kai T. Hansen 1993 Ph.D. thesis, Symbolic dynamics in chaotic systems] |

|
Kai T. Hansen
and
Predrag Cvitanović
Symbolic Dynamics and Markov Partitions for the Stadium Billiard J. Stat. Phys. ? (20??) [ chao-dyn/9502005 ] |
The archived version was accepted for publication by J. Stat. Phys. in 1996, but then I had a brilliant idea how to make it better, and a revised version is still waiting to be resubmitted. If you can bring it back to a publishable state - current version is Notes for Kai (sept 95) - please do it, and join us as a co-author. The paper is as good as most stuff that gets published, but neither of us has the time to finish it. |
[ period doubling theory | renormalization the complex plane | circle map renormalization | phase transitions ]
 
| Renormalization in chaos research overview |
| Renormalizaton theory of transitions to chaos |
  

|
Predrag Cvitanović
Universality in chaos (or, Feigenbaum for cyclists) lectures given at 1982 Zakopane School of Theoretical Physics, Acta Phys. Polonica A65, 203 (1984) [ scan by Chi-Keung Wong ] |

|
Predrag Cvitanović
and
Mogens H. Jensen
Universality in transitions to chaos in Chaos and universality (Nordita reprint selection, November 1981) |

|
Predrag Cvitanović
and
Mogens H. Jensen
Universalitet i overgang til kaos Fysisk Tidsskrift 80, 82 (1982) |
| Circle map renormalization |

|
Predrag Cvitanović
Circle maps: irrationally winding, in C. Itzykson, P. Moussa and M. Waldschmidt, eds., Number Theory and Physics, Les Houches 1989 Spring School, (Springer, New York 1992) - sorry, no figures [most of this paper is incorporated in ChaosBook.org] |

|
Predrag Cvitanović, Gemunu H. Gunaratne and M.J. Vinson
On the mode-locking universality for critical circle maps Nonlinearity 3, 873 (1990) |
|
Predrag Cvitanović,
Mogens H. Jensen, Leo P. Kadanoff and Itamar Procaccia
Renormalization, unstable manifolds and the fractal structure of mode locking Phys. Rev. Lett. 55, 343 (1985) [ DOI ] |
|
Predrag Cvitanović
Farey organization of the fractional Hall effect Phys. Scr. T9, 202 (1984) |
|
Predrag Cvitanović
Universal scaling laws for maps on the interval and circle maps in R.W. Boyd, L.M. Narducci and M.G. Raymer, eds., Instabilities and Dynamics of Lasers and Nonlinear Optical Systems, (U. of Cambridge Press, Cambridge, 1985) |
|
Predrag Cvitanović,
B. Shraiman and Bo Söderberg
Scaling laws for mode lockings in circle maps Phys. Scripta 32, 263 (1985) |
|
Predrag Cvitanović,
Mogens H. Jensen,
L.P. Kadanoff and
Itamar Procaccia
Circle maps in the complex plane in L. Pietronero and E. Tosatti, eds., Fractals in Physics, Trieste, July 1985 (North Holland, New York, 1985) |
|
Predrag Cvitanović
and
Tomas Bohr
Chaos is good news for physics Nature 329, 391-392 (1987) [ DOI ] |
|
Predrag Cvitanović
Chaos for cyclists in E. Moss, ed., Noise and Chaos in Nonlinear Dynamical Systems, (Cambridge Univ. Press, Cambridge 1989) |

|
Predrag Cvitanović
Recycling chaos in A. Ferraz, F. Oliveira and R. Osorio, eds., Nonlinear Physical Phenomena, Brasilia 1989 Winter School, (World Scientific, Singapore 1990) - sorry, no figures |

|
Predrag Cvitanović
The power of chaos in J.H. Kim and J. Stringer, eds., Applied Chaos, (John Wiley & Sons, New York 1992) - sorry, no figures |
| Renormalization theory in the complex plane |
   |
Predrag Cvitanović
and
Jan Myrheim
Complex universality Comm. Math. Phys. 121, 225 (1989) |
|
Predrag Cvitanović
and
Jan Myrheim
Universality for period n-tuplings in complex mappings Phys. Lett. 94A, 329 (1983) |
|
Predrag Cvitanović
Renormalization description of transitions to chaos in S. Lundquist, N.H. March and E. Tosatti, eds., Order and Chaos in Non-linear Physical Systems, pp. 73-97 (Plenum, New York 1988) - a subset of the "Complex Universality" paper [ DOI ] |
|
Predrag Cvitanović,
Tomas Bohr and Mogens H. Jensen
Fractal aggregates in the complex plane Europhys. Lett. 6, 445 (1988) |
| Phase transitions on fractal sets |
The discovery of phase transitions on "strange sets" was followed up by many other authors; such transitions were subsequently found in a variety of dynamical systems.

|
overview
for my group theory publications click here Group theory webbook |

|
Predrag Cvitanović
Negative dimensions and E7 symmetry Nucl. Phys. B188, 373--396 (1981) [ SPIRES citations ] |
please click here for the background story
|

|
Predrag Cvitanović
Group theory for Feynman diagrams in non-Abelian gauge theories Phys. Rev. D 14, 1536 (1976) [ INSPIRE, Google Scholar ] |
[ turbulent field theory | perturbative QED | finiteness conjecture | planar field theory | perturbative QCD | phenomenology ]
| INSPIRE citation search |
| Turbulent field theory |
Program whose goal is a non-perturbative theory of turbulent dynamics of classical,
stochastic and quantum fields. Turbulent field theory is developed in two directions:
1) explorations of the feasibility of describing weak turbulence in terms of
spatiotemporally recurrent patterns, and
2) new perturbation theory methods
for computing corrections about nontrivial saddles of path integrals.
Read the sketch paper first, click through the trace formulas papers next.
| Perturbative QED |
One big calculation, the answer
  
|
Predrag Cvitanović
and
Toichiro Kinoshita
Feynman-Dyson rules in parametric space Phys. Rev. D10, 3478 (1974) [ INSPIRE citations ] |
A (hopefully) pedagogical overview of the Schwinger and Feynman parametric representation of Feynman integrals, should be useful for any QFT perturbative calculation. Some new results, for example the theorem derived in the appendix. |
  
|
Predrag Cvitanović
and
Toichiro Kinoshita
New approach to the separation of ultraviolet and infrared divergences of Feynman-parametric integrals Phys. Rev. D10, 3991 (1974) [ INSPIRE citations ] |
A new method for dealing with Feynman diagram infrared divergences is introduced. The main result are the elegant and compact formulas (3.40) and (5.14) which extract the finite part from any general mass-shell Feynman diagram, removing both ultraviolet and infrared parts of the diagram and all of its counterterms. What remains after the projection is a pointwise-convergent integrand, well suited to numerical integrations. |
  
|
Toichiro Kinoshita
and
Predrag Cvitanović
Sixth-order radiative corrections to the electron magnetic moment Phys. Rev. Lett. 29, 1534 (1972) |
At the time perhaps the most demanding numerical computation in theoretical physics, it remained QED's most precise prediction for a number of years. A step in T. Kinoshita's heroic undertaking, but nothing you would want to read today. |
  
|
Predrag Cvitanović
and
Toichiro Kinoshita
Sixth order magnetic moment of the electron Phys. Rev. D10, 4007 (1974) [ INSPIRE citations ] |
Most of this you can safely skip, unless you happen to be evaluating (g-2) to 3-loop level. However, the new formula (6.22) for the electron magnetic moment, Sect. VI,
might be of interest: (g-2)
is evaluated from a derivative of the 2-point electron self-energy, rather than
a 3-point electron-photon vertex, with
fewer Feynman graphs: |
|
Predrag Cvitanović
Computer generation of integrands for Feynman parametric integrals Cornell preprint CLNS-234 (June, 1973) and Proc. 3rd Coll. on Advanced Comp. Meth. in Theoretical Physics (Marseille, 1973) |
| Finiteness of gauge field theories |
For me the conceptually most striking lesson of these long QED calculations were the amazing cancellations induced by gauge invariance. The desire to understand and exploit gauge invariance more effectively has motivated much of my subsequent research. The most interesting results of this effort were the mass-shell QCD Ward identities and the construction of the QCD gauge sets. This work also motivated the formulation of planar field theory.
Other papers in this series are those on the QCD mass-shell infrared singularities and the diagram counting, both attempts to formulate gauge-invariant models computable to high orders, in order to investigate the nature of gauge-invariance induced cancellations.
   
|
Predrag Cvitanović
Asymptotic estimates and gauge invariance Nucl. Phys. B127, 176 (1977) [ INSPIRE citations ] |
On basis of very skimpy numerical evidence, I conjecture that the gauge invariance induced cancellations
are so dramatic that the growth rate of
high order perturbation theory corrections to mass-shell gauge-invariant
quantities is slower than Dyson's asymptotic series n! estimate.
In the case of QED vertex corrections, the smallest gauge invariant set
contributing to (m+m'+k)th order
consists of m photon "strands" attached to the incoming
electron,
m' photon "strands" attached to the outgoing electron, and
k photon "strands" crossing the external photon vertex.
Ignoring sets with electron loops and
assuming that each gauge set gives a finite contribution
leads to a guess that perturbation series for
the electron magnetic moment sums up to approximately
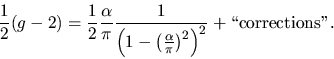
|
| Planar field theory |
The method that I have used to develop the planar field theory is somewhat different from what is in most field theory textbooks; consulting my Field Theory webbook might make this derivation more accessible.
  
|
Predrag Cvitanović
Planar perturbation expansion Phys. Lett. B99, 49 (1981) [ INSPIRE citations ] |
  
|
Predrag Cvitanović
The planar sector of field theories (with P.G. Lauwers and P.N. Scharbach), Nucl. Phys. B203, 385 (1982) [ INSPIRE citations ] |
Though the formalism is rather different, essentially the same theory was rederived in 1994 by M.A. Douglas, R. Gopakumar and David J. Gross, D.V. Voiculescu, in 1998 by 't Hooft, and many others. R. Speicher (13 Apr 2014): "In a sense some aspects of this theory of freeness were anticipated (but mostly neglected) in the physics community in [this] paper" |
| Perturbative QCD |

|
Predrag Cvitanović
Yang-Mills theory of the mass-shell Phys. Rev. Lett. 37, 1528 (1976) [ INSPIRE citations ] |
Mass-shell amplitudes for both QED and QCD are defined via dimensional regularization, and shown to to be gauge invariant trough a cancellation between UL and IR singularities. Prior to this article, IR and UR were regularized by different methods which, when applied to QCD, violated gauge invariance. |

|
Predrag Cvitanović
Infra-red structure of Yang-Mills theories Phys. Lett. 65B, 272 (1976) [ INSPIRE citations ] |

|
Predrag Cvitanović
Quantum Chromodynamics on the mass-shell Nucl. Phys. B130, 114 (1977) [ INSPIRE citations ] |

|
Predrag Cvitanović, Benny Lautrup and R.B. Pearson
The number and weights of Feynman diagrams Phys. Rev. D18, 1939 (1978) [ INSPIRE citations ] |
|
Predrag Cvitanović, Jeff Greensite and Benny Lautrup
The cross-over points in lattice gauge theories with continuous gauge groups Phys. Lett. 105B, 201 (1981) [ INSPIRE citations ] |

|
Predrag Cvitanović, P.G. Lauwers and P.N. Scharbach
Gauge invariance structure of Quantum Chromodynamics Nucl. Phys. B186, 165 (1981) [ INSPIRE citations ] |
| Phenomenology etc. |

|
Predrag Cvitanović
Spin and parity from crossections and angular distributions, in J. Bjorken et al., Notes from the SLAC Theory Workshop on the Psi, SLAC-PUB-1515 , (Dec. 7, 1974) |
|
Predrag Cvitanović
Wide-angle behavior of a double-scattering diagram Phys. Rev. D10, 338 (1974) |
|
Predrag Cvitanović, R.J. Gonsales and D.E. Neville
Color charge algebras in Adler's Chromodynamics Phys. Rev. D18, 3881 (1978) |
|
Predrag Cvitanović, P. Hoyer and K. Konishi
Partons and branching Phys. Lett. 85B 413 (1979) |
|
Predrag Cvitanović and R. Horsley
Exact solutions of the Altarelli-Parisi equations Nucl. Phys. B173, 229 (1980) |
|
Predrag Cvitanović, Poul Hoyer and K. Zalewski
Parton evolution as a branching process Nucl. Phys. B176, 429 (1980) [ INSPIRE citations ] |
| Miscelaneous |
|
|
Predrag Cvitanović et al
drafts in progress (of interest only to frustrated collaborators) |

|
Predrag Cvitanović
Midnight rider Bike World (August 1974) |
 |
Predrag Cvitanović and Mitchell J. Feigenbaum,
for David Bensimon, Thomas C. Halsey, Mogens H. Jensen,
Leo P. Kadanoff, Albert Libchaber, Itamar Procaccia, Boris I. Shraiman and
Joel Stavans
More on microcanonical paradigm (Göteborg, 3 a.m. of 17 Nov. 1985), rejected from every proceedings submitted to. |